INTRODUCTION TO THE BRAYTON CYCLE IN GAS TURBINES

The purpose of this white papers on the Brayton Thermodynamic Cycle is to provide a fairly non-technical introduction to the most important thermodynamic cycle used in the gas turbine technology used by AscenTrust, LLC. (The Company) in the design and installation of the first phase of the Nuclear Technology Pebble Bed Modular Reactor (NTPBMR) prototype project.  The NTPBMR power plant will eventually use a very unique type of turbine cycle: The closed-loop, Brayton cycle helium turbine.  In order to realize this new technology, the Company will first build conventional, natural-gas fired power plants connected to an existing natural gas pipeline.  Phase two will be to build conventional natural-gas fired power plants powered by LNG (Liquid Natural Gas).  Phase three of the project will consist of building a combustion chamber to heat the helium to be used in a closed-cycle turbine which will be design in our research and development center. The 55MWe closed-loop, helium powered gas turbine, will then form the basis for the Balance of Plant for the 110MWe helium-cooled, graphite-moderated, pebble bed nuclear power plant. 

In order to introduce the operations of a gas turbine we will have to review some basic concepts of thermodynamics which were developed in the days of Joules and Carnot and are of interest to anyone who has an interest in understanding the processes involved  in the production of electricity through the use of thermal energy.  The source of thermal energy is the subject of other white papers in this series.  The final resting place of the source of thermal energy for our project is of course the production of energy through the use of nuclear power. Inherent in any discussion of thermodynamics is the requirement for a basic understanding of the structure of matter,  and certainly in the discussion of the production of electrical energy through the fission of nuclear material are some of the topics of modern physics: Quantum Mechanics and Special Relativity.  Very little will be said in this paper concerning these two vast topics of Physics and Engineering.  Even the statistical nature of thermodynamics will not be mentioned.

A gas turbine, also called a combustion turbine, is a rotary engine that extracts energy from a flow of combustion gas. The main components of a gas turbine are: an upstream compressor coupled to a downstream turbine, and a combustion chamber in-between. Energy is added to the gas stream in the combustor, where fuel is mixed with air and ignited. In the high pressure environment of the combustor, combustion of the fuel increases the temperature. The products of the combustion are forced into the turbine section. There, the high velocity and volume of the gas flow is directed through a nozzle over the turbine's blades, spinning the turbine which powers the compressor and, for some turbines, drives their mechanical output. The energy given up to the turbine comes from the reduction in the temperature of the exhaust gas. Energy is extracted in the form of shaft power, compressed air and thrust, in any combination, and used to power aircraft, trains, ships, generators, and even tanks.

SECTION ONE: CHARACTERISTICS OF THE BRAYTON CYCLE

1.  INTRODUCTION: The Brayton cycle was first proposed by George Brayton for use in the reciprocating oil-burning engine that he developed around 1870. Today, it is used for gas turbines only where both the compression and expansion processes take place in rotating machinery. Both the compressors and the turbine are axial machines.

Gas turbines usually operate on an open cycle, as shown in Fig. 1.1 below. Fresh air at ambient conditions is drawn into the compressor, where its temperature and pressure are raised. The high pressure air proceeds into the combustion chamber, where the fuel is burned at constant pressure. The resulting high temperature gases then enter the turbine, where they expand to the atmospheric pressure while producing power. The exhaust gases leaving the turbine are thrown out (not recirculated), causing the cycle to be classified as an open cycle. The open gas-turbine cycle described above can be modeled as a closed cycle, as shown in Fig. 1.2, by utilizing the air-standard assumptions. Here the compression and expansion processes remain the same, but the combustion process is replaced by a constant-pressure heat-addition process from an external source, and the exhaust process is replaced by a constant pressure heat-rejection process to the ambient air. The ideal cycle that the working fluid undergoes in this closed loop is the Brayton cycle, which is made up of four internally reversible processes:

• 1-2 Isentropic compression (in a compressor)
• 2-3 Constant-pressure heat addition
• 3-4 Isentropic expansion (in a turbine)
• 4-1 Constant-pressure heat rejection

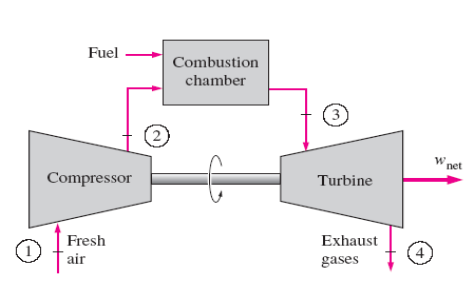
FIGURE 1.1. OPEN CYCLE GAS TURBINE

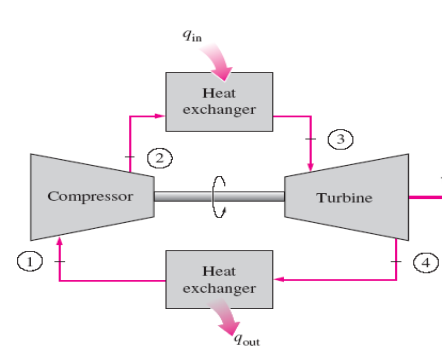
FIGURE 1.2.  CLOSED-CYCLE GAS TURBINE

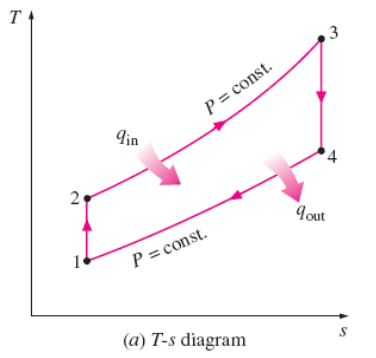
FIGURE 1.3(a). TEMPERATURE-ENTROPY DIAGRAM FOR BRAYTON CYCLE

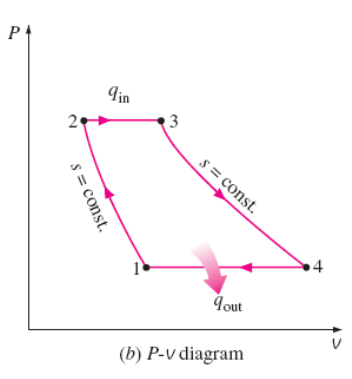
FIGURE 1.3 (b).  PRESSURE-VOLUME DIAGRAM FOR BRAYTON CYCLE

2.    Brayton Cycle Temperature:  The highest temperature in the cycle occurs at the end of the combustion process (state 3), and it is limited by the maximum temperature that the turbine blades can withstand. This also limits the pressure ratios that can be used in the cycle. There should be a compromise between the pressure ratio (thus the thermal efficiency) and the net work output. With less work output per cycle, a larger mass flow rate (thus a larger system) is needed to maintain the same power output, which may not be economical. In most common designs, the pressure ratio of gas turbines ranges from about 11 to 16.

3.    Air in Gas Turbines:  The air in gas turbines performs two important functions: It supplies the necessary oxidant for the combustion of the fuel, and it serves as a coolant to keep the temperature of various components within safe limits. The second function is accomplished by drawing in more air than is needed for the complete combustion of the fuel. In gas turbines, an air–fuel mass ratio of 50 or above is not uncommon. Therefore, in a cycle analysis, treating the combustion gases as air does not cause any appreciable error. Also, the mass flow rate through the turbine is greater than that through the compressor, the difference being equal to the mass flow rate of the fuel. Thus, assuming a constant mass flow rate throughout the cycle yields conservative results for open-loop gas-turbine engines.

4.     Main Applications of Open-Cycle Gas Turbines:  The two major application areas of gas-turbine engines are aircraft propulsion and electric power generation. When it is used for aircraft propulsion, the gas turbine produces just enough power to drive the compressor and a small generator to power the auxiliary equipment. The high-velocity exhaust gases are responsible for producing the necessary thrust to propel the aircraft.

5.    Combined-Cycle Gas Turbines: Gas turbines are also used as stationary power plants to generate electricity as stand-alone units or in conjunction with steam power plants on the high-temperature side. In these plants, the exhaust gases of the gas turbine serve as the heat source for the steam.

6.    Closed-Cycle, Helium, Gas Turbines: The gas-turbine  cycle can also be executed as a closed cycle for use in nuclear power plants. This time the working fluid is not limited to air, and a gas with more desirable characteristics (such as helium) can be used.

7.    The majority of the Western world’s naval fleets already use gas-turbine engines for propulsion and electric power generation. The General Electric LM2500 gas turbines used to power ships have a simple-cycle thermal efficiency of 37 percent. Many modern marine propulsion systems use gas turbines together with diesel engines because of the high fuel consumption of simple-cycle gas-turbine engines. In combined diesel and gas-turbine systems, diesel is used to provide for efficient low-power and cruise operation, and gas turbine is used when high speeds are needed.

8.    The General Electric WR-21 gas turbines equipped with inter-cooling and regeneration have a thermal efficiency of 43 percent and produce 21.6 MW (29040 hp). The regeneration also reduces the exhaust temperature from 600°C to 350°C. Air is compressed to 3 atm before it enters the intercooler. Compared to steam-turbine and diesel propulsion systems, the gas turbine offers greater power for a given size and weight, high reliability, long life, and more convenient operation. The engine start-up time has been reduced from 4 h required for a typical steam propulsion system to less than 2 min for a gas turbine.

9.    In gas-turbine power plants, the ratio of the compressor work to the turbine work, called the back work ratio, is very high. Usually more than one-half of the turbine work output is used to drive the compressor. The situation is even worse when the isentropic efficiencies of the compressor and the turbine are low. This is quite in contrast to steam power plants, where the back work ratio is only a few percent. This is not surprising, however, since a liquid is compressed in steam power plants instead of a gas, and the steady-flow work is proportional to the specific volume of the working fluid. A power plant with a high back work ratio requires a larger turbine to provide the additional power requirements of the compressor. Therefore, the turbines used in gas-turbine power plants are larger than those used in steam power plants of the same net power output.

SECTION TWO: DEVELOPMENTS IN BRAYTON CYCLE FOR GAS TURBINES

The gas turbine has experienced phenomenal progress and growth since its first successful development in the 1930s. The early gas turbines built in the 1940s and even 1950s had simple cycle efficiencies of about 17 percent because of the low compressor and turbine efficiencies and low turbine inlet temperatures due to metallurgical limitations of those times. Therefore, gas turbines found only limited use despite their versatility and their ability to burn a variety of fuels. The efforts to improve the cycle efficiency concentrated in three areas:

1. Increasing the turbine inlet (or firing) temperatures This has been the primary approach taken to improve gas-turbine efficiency. The turbine inlet temperatures have increased steadily from about 540°C in the 1940s to 1425°C and even higher today. These increases were made possible by the development of new materials and the innovative cooling techniques for the critical components such as coating the turbine blades with ceramic layers and cooling the blades with the discharge air from the compressor. Maintaining high turbine inlet temperatures with an air-cooling technique requires the combustion temperature to be higher to compensate for the cooling effect of the cooling air. However, higher combustion temperatures increase the amount of nitrogen oxides (NOx), which are responsible for the formation of ozone at ground level and smog. Using steam as the coolant allowed an increase in the turbine inlet temperatures by 200°F without an increase in the combustion temperature. Steam is also a much more effective heat transfer medium than air.

2. Increasing the efficiencies of turbomachinery components: The performance of early turbines suffered greatly from the inefficiencies of turbines and compressors. However, the advent of computers and advanced techniques for computer-aided design made it possible to design these components aerodynamically with minimal losses. The increased efficiencies of the turbines and compressors resulted in a significant increase in the cycle efficiency.

3. Adding modifications to the basic cycle: The simple-cycle efficiencies of early gas turbines were practically doubled by incorporating inter-cooling, regeneration (or recuperation), and reheating, discussed in the next two sections. These improvements, of course, come at the expense of increased initial and operation costs, and they cannot be justified unless the decrease in fuel costs offsets the increase in other costs. The relatively low fuel prices, the general desire in the industry to minimize installation costs, and the tremendous increase in the simple-cycle efficiency to about 40 percent left little desire for opting for these modifications. The first gas turbine for an electric utility was installed in 1949 in Oklahoma as part of a combined-cycle power plant. It was built by General Electric and produced 3.5 MW of power. Gas turbines installed until the mid-1970s suffered from low efficiency and poor reliability. In the past, the base-load electric power generation was dominated by large coal and nuclear power plants.

4.    Shift to Natural Gas-fired gas turbines:  There has been a historic shift toward natural gas–fired gas turbines because of their higher efficiencies, lower capital costs, shorter installation times, and better emission characteristics, and the abundance of natural gas supplies, and more and more electric utilities are using gas turbines for base-load power production as well as for peaking. The construction costs for gas-turbine power plants are roughly half that of comparable conventional fossil-fuel steam power plants, which were the primary base-load power plants until the early 1980s. More than half of all power plants to be installed in the foreseeable future are forecast to be gas turbine or combined gas–steam turbine types.

5.    Example of increase in efficiency and power of gas turbines:  A gas turbine manufactured by General Electric in the early 1990s had a pressure ratio of 13.5 and generated 135.7 MW of net power at a thermal efficiency of 33 percent in simple-cycle operation. A more recent gas turbine manufactured by General Electric uses a turbine inlet temperature of 1425°C and produces up to 282 MW while achieving a thermal efficiency of 39.5 percent in the simple-cycle mode. A 1.3-ton small-scale gas turbine labeled OP-16, built by the Dutch firm Opra Optimal Radial Turbine, can run on gas or liquid fuel and can replace a 16-ton diesel engine. It has a pressure ratio of 6.5 and produces up to 2 MW of power. Its efficiency is 26 percent in the simple-cycle operation, which rises to 37 percent when equipped with a regenerator.

SECTION THREE: THE BRAYTON CYCLE WITH REGENERATION

In gas-turbine engines, the temperature of the exhaust gas leaving the turbine is often considerably higher than the temperature of the air leaving the compressor. Therefore, the high pressure air leaving the compressor can be heated by transferring heat to it from the hot exhaust gases in a counter-flow heat exchanger, which is also known as a regenerator or a recuperator. A sketch of the gas-turbine engine utilizing a regenerator and the T-s diagram of the new cycle are shown in in the figures below:

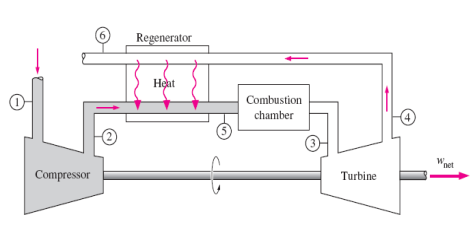
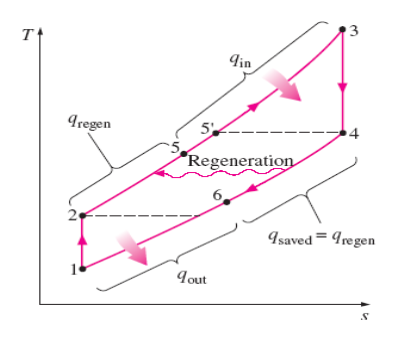
The thermal efficiency of the Brayton cycle increases as a result of regeneration since the portion of energy of the exhaust gases that is normally rejected to the surroundings is now used to preheat the air entering the combustion chamber. This, in turn, decreases the heat input (thus fuel) requirements for the same net work output. Note, however, that the use of a regenerator is recommended only when the turbine exhaust temperature is higher than the compressor exit temperature. Otherwise, heat will flow in the reverse direction (to the exhaust gases), decreasing the efficiency. This situation is encountered in gas-turbine engines operating at very high pressure ratios.

The highest temperature occurring within the regenerator is T4, the temperature of the exhaust gases leaving the turbine and entering the regenerator. Under no conditions can the air be preheated in the regenerator to a temperature above this value. Air normally leaves the regenerator at a lower temperature, T5. In the limiting (ideal) case, the air exits the regenerator at the inlet temperature of the exhaust

SECTION FOUR: THE BRAYTON CYCLE WITH INTERCOOLING, REHEATING, AND REGENERATION

4.1.     Multistage Compression with Intercooling: The net work of a gas-turbine cycle is the difference between the turbine work output and the compressor work input, and it can be increased by either decreasing the compressor work or increasing the turbine work, or both. As mentioned before that the work required to compress a gas between two specified pressures can be decreased by carrying out the compression process in stages and cooling the gas in between —that is, using multistage compression with intercooling.  As the number of stages is increased, the compression process becomes nearly isothermal at the compressor inlet temperature, and the compression work decreases.

4.2.     Multistage Expansion with re-heating: Likewise, the work output of a turbine operating between two pressure levels can be increased by expanding the gas in stages and reheating it in between—that is, utilizing multistage expansion with reheating. This is accomplished without raising the maximum temperature in the cycle. As the number of stages is increased, the expansion process becomes nearly isothermal. The foregoing argument is based on a simple principle:

4.3.     Intercooling and Re-heat:  The steady-flow compression or expansion work is proportional to the specific volume of the fluid. Therefore, the specific volume of the working fluid should be as low as possible during a compression process and as high as possible during an expansion process. This is precisely what intercooling and reheating accomplish. Combustion in gas turbines typically occurs at four times the amount of air needed for complete combustion to avoid excessive temperatures. Therefore, the exhaust gases are rich in oxygen, and reheating can be accomplished by simply spraying additional fuel into the exhaust gases between two expansion states.

The working fluid leaves the compressor at a lower temperature, and the turbine at a higher temperature, when intercooling and reheating are utilized. This makes regeneration more attractive since a greater potential for regeneration exists. Also, the gases leaving the compressor can be heated to a higher temperature before they enter the combustion chamber because of the higher temperature of the turbine exhaust.

A schematic of the physical arrangement and the T-s diagram of an ideal two-stage gas-turbine cycle with intercooling, reheating, and regeneration are shown in the figures below:

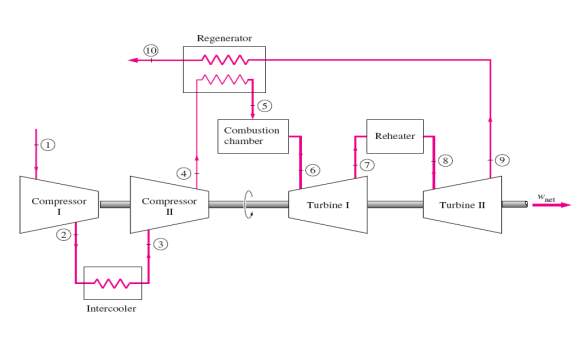
FIGURE 4(a).  DIAGRAM OF TWO STAGE TURBINE WITH INTERCOOLING, REHEATING AND REGENERATION

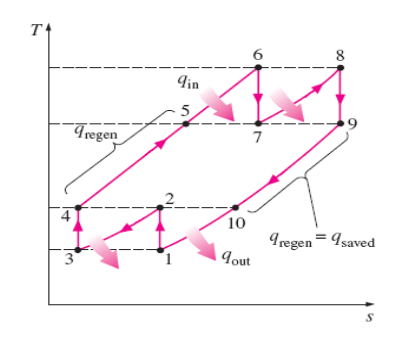
FIGURE 4(b).  TEMPERATURE/ENTROPY DIAGRAM, TWO STAGE TURBINE WITH INTERCOOLING, REHEATING AND REGENERATION

The gas enters the first stage of the compressor at state 1, is compressed isentropically to an intermediate pressure P2, is cooled at constant pressure to state 3 (T3 = T1), and is compressed in the second stage isentropically to the final pressure P4. At state 4 the gas enters the regenerator, where it is heated to T5 at constant pressure. In an ideal regenerator, the gas leaves the regenerator at the temperature of the turbine exhaust, that is, T5 = T9. The primary heat addition (or combustion) process takes place between states 5 and 6. The gas enters the first stage of the turbine at state 6 and expands isentropically to state 7, where it enters the reheater. It is reheated at constant pressure to state 8 (T8 = T6), where it enters the second stage of the turbine. The gas exits the turbine at state 9 and enters the regenerator, where it is cooled to state 10 at constant pressure. The cycle is completed by cooling the gas to the initial state (or purging the exhaust gases).

SECTION FIVE:  IDEAL JET-PROPULSION CYCLES

5.1.    Introduction:  Gas-turbine engines are widely used to power aircraft because they are light and compact and have a high power-to-weight ratio. Aircraft gas turbines operate on an open cycle called a jet propulsion cycle. The ideal jet propulsion cycle differs from the simple ideal Brayton cycle in that the gases are not expanded to the ambient pressure in the turbine. Instead, they are expanded to a pressure such that the power produced by the turbine is just sufficient to drive the compressor and the auxiliary equipment, such as a small generator and hydraulic pumps. 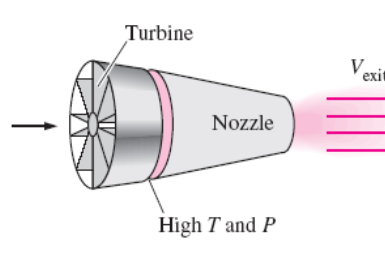That is, the net work output of a jet propulsion cycle is zero. The gases that exit the turbine at a relatively high pressure are subsequently accelerated in a nozzle to provide the thrust to propel the aircraft (See figure below).

Also, aircraft gas turbines operate at higher pressure ratios (typically between 10 and 25), and the fluid passes through a diffuser first, where it is decelerated and its pressure is increased before it enters the compressor. Aircraft are propelled by accelerating a fluid in the opposite direction to motion. This is accomplished by either slightly accelerating a large mass of fluid ( propeller-driven engine) or greatly accelerating a small mass of fluid ( jet or turbojet engine) or both (turboprop engine). A  schematic of a turbojet engine and the T-s diagram of the ideal turbojet cycle are shown in the figures below:

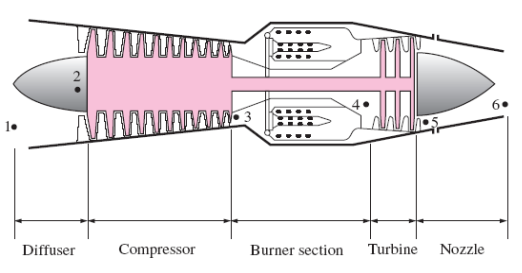
FIGURE 5 (a): SCHEMATIC OF A TURBOJET ENGINE

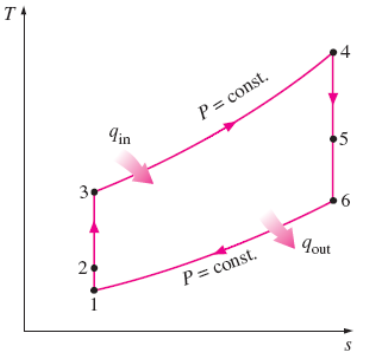
FIGURE 5(b): TEMPERATURE-ENTROPY DIAGRAM FOR THE TURBOJET CYCLE

The pressure of air rises slightly as it is decelerated in the diffuser. Air is compressed by the compressor. It is mixed with fuel in the combustion chamber, where the mixture is burned at constant pressure. The high-pressure and high-temperature combustion gases partially expand in the turbine, producing enough power to drive the compressor and other equipment. Finally, the gases expand in a nozzle to the ambient pressure and leave the engine at a high velocity. In the ideal case, the turbine work is assumed to equal the compressor work. Also, the processes in the diffuser, the compressor, the turbine, and the nozzle are assumed to be isentropic. In the analysis of actual cycles, however, the irreversibilities associated with these devices should be considered. The effect of the irreversibilities is to reduce the thrust that can be obtained from a turbojet engine. The thrust developed in a turbojet engine is the unbalanced force that is caused by the difference in the momentum of the low-velocity air entering the engine and the high-velocity exhaust gases leaving the engine, and it is determined from Newton’s second law.

SECTION SIX: TURBOFAN ENGINES

The first airplanes built were all propeller-driven, with propellers powered by engines essentially identical to automobile engines. The major breakthrough in commercial aviation occurred with the introduction of the turbojet engine in 1952. Both propeller-driven engines and jet-propulsion driven engines have their own strengths and limitations, and several attempts have been made to combine the desirable characteristics of both in one engine. The most widely used engine in aircraft propulsion is the turbofan (or fanjet) engine wherein a large fan driven by the turbine forces a considerable amount of air through a duct (cowl) surrounding the engine, as shown in the figures below.

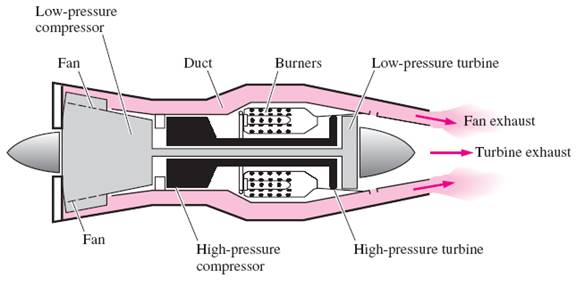
FIGURE 6(a): SCHEMATIC OF A TURBOFAN AIRCRAFT ENGINE

The fan exhaust leaves the duct at a higher velocity, enhancing the total thrust of the engine significantly. A turbofan engine is based on the principle that for the same power, a large volume of slower moving air produces more thrust than a small volume of fast-moving air.

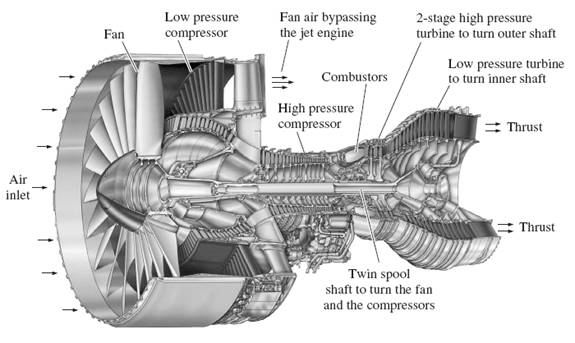
FIGURE 6(b): SECTION OF A MODERN TURBOFAN JET ENGINE

The jet engine shown above is used to power the Boeing 777 aircraft. This is a Pratt & Whitney PW4084 turbofan capable of producing 84,000 pounds of thrust. It is 4.87 m (192 in.) long, has a 2.84 m (112 in.) diameter fan, and it weighs 6800 kg (15,000 lbm).

The turbofan engine on an airplane can be distinguished from the less efficient turbojet engine by its fat cowling covering the large fan. All the thrust of a turbojet engine is due to the exhaust gases leaving the engine at about twice the speed of sound. In a turbofan engine, the high-speed exhaust gases are mixed with the lower-speed air, which results in a considerable reduction in noise.

New cooling techniques have resulted in considerable increases in efficiencies by allowing gas temperatures at the burner exit to reach over 1500°C, which is more than 100°C above the melting point of the turbine blade materials. Turbofan engines deserve most of the credit for the success of jumbo jets that weigh almost 400,000 kg and are capable of carrying over 400 passengers for up to a distance of 10,000 km at speeds over 950 km/h with less fuel per passenger mile.

The ratio of the mass flow rate of air bypassing the combustion chamber to that of air flowing through it is called the bypass ratio. The first commercial high-bypass-ratio engines had a bypass ratio of 5. Increasing the bypass ratio of a turbofan engine increases thrust. Thus, it makes sense to remove the cowl from the fan. The result is a propjet engine.

Turbofan and propjet engines differ primarily in their bypass ratios: 5 or 6 for turbofans and as high as 100 for propjets. As a general rule, propellers are more efficient than jet engines, but they are limited to low-speed and low-altitude operation since their efficiency decreases at high speeds and altitudes.